17. ให้  \((a+\frac{1}{a})^{3}=9\) แล้ว \((a^{2}+\frac{1}{a^{2}}+2)^{3}\) เท่ากับข้อใดต่อไปนี้

1. 27
2. 81
3. 243
4. 729

วิธีทำ

ข้อนี้ต้องใช้ พวกผลบวกกำลังสามเข้ามาช่วยคับ เริ่มจากการกระจาย สมการที่โจทย์ให้มาก่อนเลยคือ

\((a+\frac{1}{a})^{3}=9\)

ซึ่งเราจะได้ว่า \((a+\frac{1}{a})=9^{\frac{1}{3}}\) เก็บไว้ก่อน เผื่อได้ใช้

ต่อไปเอาก้อนนี้  \((a+\frac{1}{a})^{3}\) โดยใช้สูตรกำลังสามสมบูรณ์ ใครจำสูตรไม่ได้ดูรูปเอาเด้อ

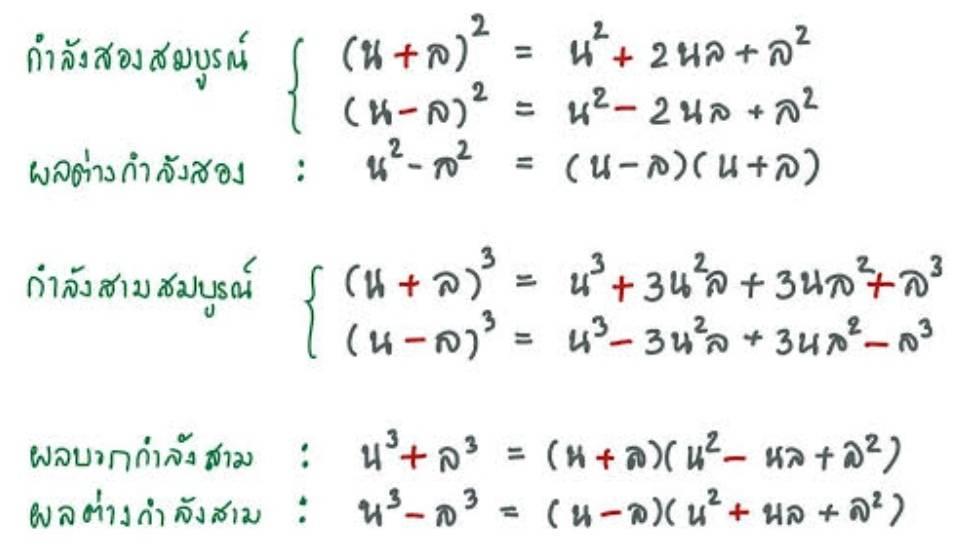
จะได้

\begin{array}{lcl}(a+\frac{1}{a})^{3}&=&9\\a^{3}+3a^{2}\frac{1}{a}+3a\frac{1}{a^{2}}+\frac{1}{a^{3}}&=&9\\a^{3}+\frac{1}{a^{3}}+3(a+\frac{1}{a})&=&9\\a^{3}+\frac{1}{a^{3}}+3\cdot 9^{\frac{1}{3}}&=&9\\a^{3}+\frac{1}{a^{3}}&=&9-3\cdot 9^{\frac{1}{3}}\\(a+\frac{1}{a})(a^{2}-a\cdot\frac{1}{a}+\frac{1}{a^{2}}&=&9-3\cdot 9^{\frac{1}{3}}\\(a+\frac{1}{a})(a^{2}+\frac{1}{a^{2}}-1)&=&9-3\cdot 9^{\frac{1}{3}}\\(9^{\frac{1}{3}})(a^{2}+\frac{1}{a^{2}}-1)&=&9-3\cdot 9^{\frac{1}{3}}\\(a^{2}+\frac{1}{a^{2}}-1)&=&\frac{9-3\cdot 9^{\frac{1}{3}}}{9^{\frac{1}{3}}}\\a^{2}+\frac{1}{a^{2}}-1+3&=&\frac{9-3\cdot 9^{\frac{1}{3}}}{9^{\frac{1}{3}}}+3\\a^{2}+\frac{1}{a^{2}}+2&=&3^{\frac{4}{3}}\\(a^{2}+\frac{1}{a^{2}}+2)^{3}&=&(3^{\frac{4}{3}})^{3}\\(a^{2}+\frac{1}{a^{2}}+2)^{3}&=&3^{4}\\(a^{2}+\frac{1}{a^{2}}+2)^{3}&=&81\end{array}